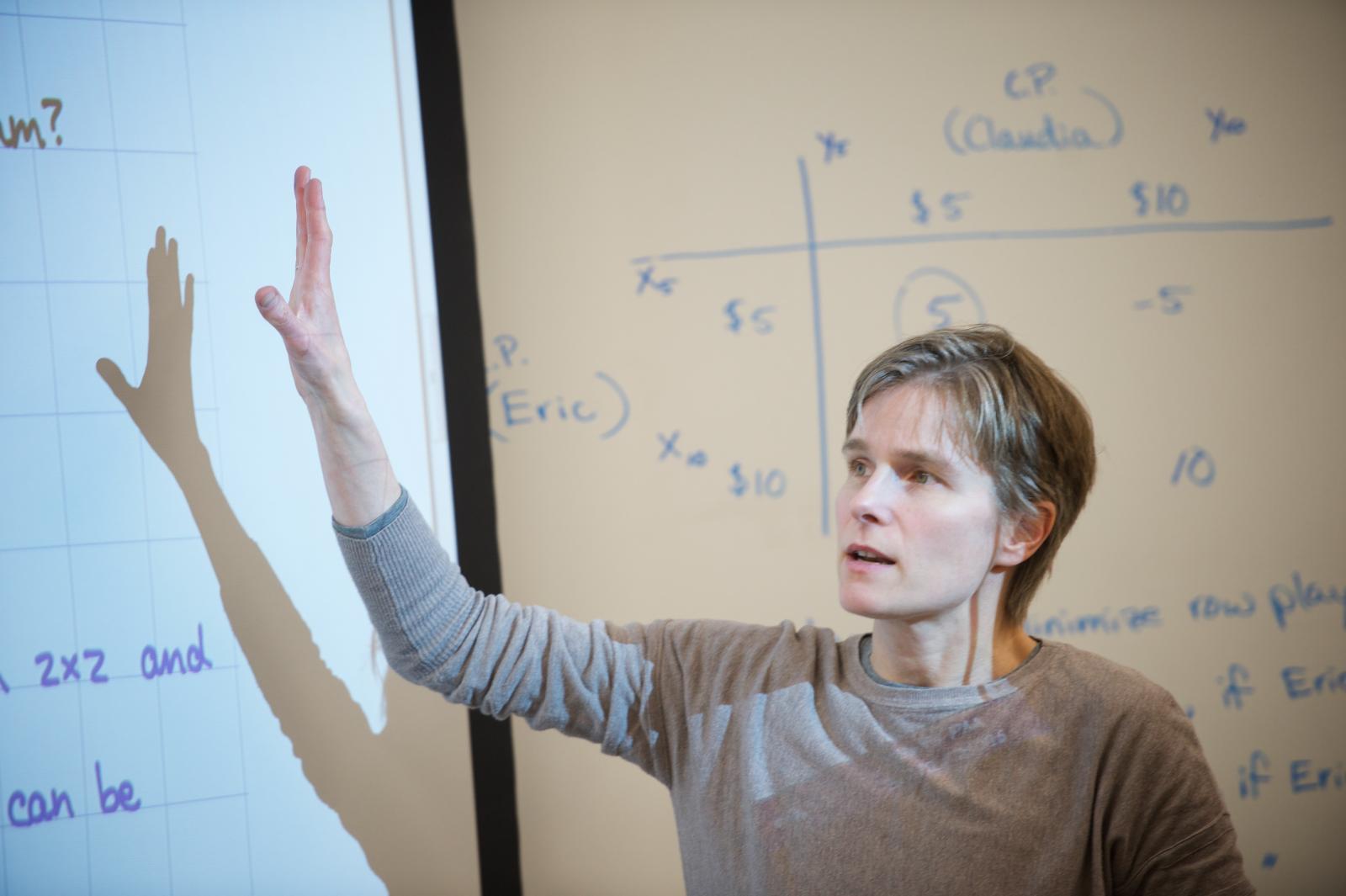Current students: Declare this program
Once you’re admitted as an undergraduate student and have met any further admission requirements your chosen program may have, you may declare a major or declare an optional minor.
Future students: Apply now
Apply to Metro State: Start the journey toward your Industrial & Applied Mathematics BS now. Learn about the steps to enroll or, if you have questions about what Metro State can offer you, request information, visit campus or chat with an admissions counselor.
Get started on your Industrial & Applied Mathematics BS
More ways to earn your degree: Metro State offers the flexibility you need to finish your degree. Through programs at our partner institutions, you can find a path to getting your Industrial & Applied Mathematics BS that works best for you.
Program eligibility requirements
Students expressing interest in the Industrial & Applied Mathematics Bachelor of Science when they apply for admission to the university will be assigned a faculty advisor in the Department of Mathematics & Statistics and will be given premajor status.
Students interested in pursuing this program should take the following steps:
- Speak with a faculty member in the Mathematics & Statistics Department or contact the Chair of the department (math@metrostate.edu) to learn more about the Industrial & Applied Mathematics, B.S. as well as other programs in the department to determine which program best aligns with your interests.
- Complete the following Premajor Requirements:
- Take the following prerequisite courses: STAT 201 Statistics I, ICS 140 Introduction to Computational Thinking with Programming, MATH 210 Calculus I, and MATH 215 Discrete Mathematics.
- Earn grades of C- or higher and a cumulative GPA of 2.5 or higher in the above prerequisite courses.
- Declare the Industrial & Applied Mathematics, B.S. using the online Undergraduate Program Change or Declaration eForm.
Transfer coursework equivalency is determined by the Mathematics and Statistics Department.